What Delta is and Why it Matters

This is a deep dive into Delta to define delta officially, explain that in laments terms, and also to introduce the idea of delta being used as a probability.

What is a 'Delta?"
We have to start with the definition from the Chicago Board Options Exchange (CBOE), but don't worry if this doesn't make any sense, after this formal description, we will explain what delta means in English.

Officially: Delta
The amount by which an option's price will change for a one-point change in price by the underlying entity.

In English

• A 90-delta option will move about $0.90 for the next $1 move in stock price.
• A 50-delta option will move about $0.50 for the next $1 move in stock price.
• A 10-delta option will move about $0.10 for the next $1 move in stock price.

Broadly speaking, 'Delta' measures how far an option is in (or out) of the money and therefore how much it will move for every $1 move in stock price.

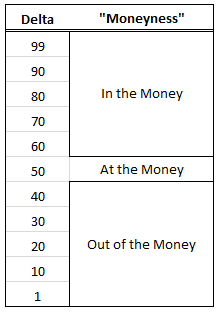
Delta ranges from 0 to 100. The larger the absolute value of delta, the further in the money an option is. In English:

If an option has a delta near 100, it is deep in the money.
If an option has a delta that is near 0, it is far out of the money.
If an option has a delta near 50, it is near the money (at the money).

Real World Example on November 29th, 2016
Apple Inc (NASDAQ:AAPL) Stock price in this example is $111.74. Now, let's look at the deltas, strike prices and option prices for a month of options:

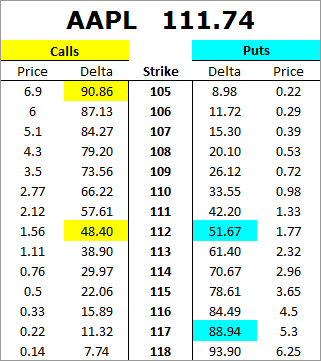
First, on the left hand side (in yellow) we see all of the call options.

Second, on the right hand side (in blue) we see all of the put options.

Next to the strike prices, we see the deltas. Let's dive in and focus on one strike price: 105

Stock Price: $111.74

1. The 105 strike call option has a delta of 90.86. This number represents that the 105 call option is deep in the money.

2. The 105 strike put option has a delta of 8.98. This number represents that the 105 put option is far out of the money.

Next, let's focus on the 117 strike.

1. The 117 strike call option has a delta of 11.32. This number represents that the 117 call option is far out of the money.

2. The 117 strike put option has a delta of 88.94. This number represents that the 117 put option is deep in the money.

For completeness, we can look at the options that are at the money.

1. The 112 strike call option has a delta of 48.40. This number represents that the 112 call option is near the money.

2. The 112 strike put option has a delta of 51.67. This number represents that the 112 put option is deep near the money.

Real World Application in CML Backtester
This is a print out from the CMLviz Option Back-tester:

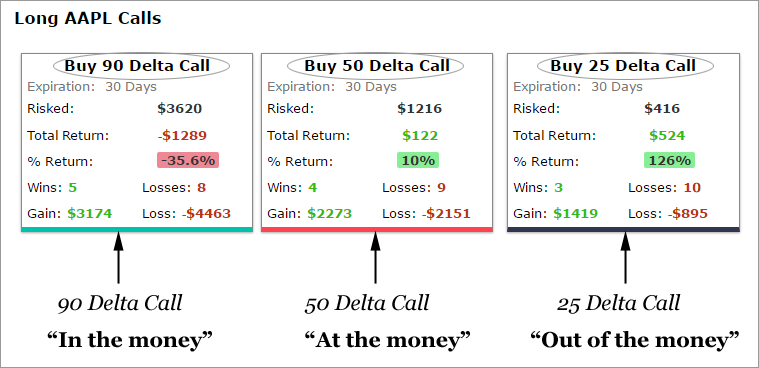
This example is a one-year back-test, trading every 30 days, for buying a call in AAPL. We can see:

• Buying the 90 delta call (in the money) every 30-days, lost 35.6% over one-year.

• Buying the 50 delta call (at the money) every 30-days, gained 10% over one-year.

• Buying the 25 delta call (out of the money) every 30-days, gained 126% over one-year.

How This Works
(i) The back-tester looks one-year ago, and buys the appropriate delta call option (90, 50 and 25).

(ii) Every 30-days, the backtester sells that call, records the profit or loss, then buys the appropriate delta call option on the new date (90, 50 and 25) again.

(iii) The back-tester repeats this process for a year, trading every 30 days and then presents the results.

Note: The backtester can go back as far as three-years and can trade as frequently as you desire (even weekly options) and can choose any deltas you want.

DELTA AS A PROBABILITY

Transcript: I want to introduce the idea of Delta as a probability. Some of you may know this, some of you may not, but a 50 delta option, which is at the money option, has about a 50% chance of being in the money. So Delta can be used as a probability in the short term, and if you're wondering why not in the long term, it's a difference between the normal distribution and the log normal distribution in short periods of time. Those two distributions are very similar, but you can go further. What are the odds? At any one time that a stock goes to a 25 delta put about 25% said differently. There's a 75% chance the stock never gets here. And if our loss starts right around 20 delta, it depends on the options. This trade should have between a 75 and 80% win rate because there's about an 80% chance that this never happens. Or if you prefer there's a 20% chance this happens. 20% is big enough that we want to cover this trade. We don't want to be naked short. So this trade should have from there to there is positive. Anything from here over we should make money. This trade should make money. That should be about 75 or 80% of the time.

A '30 delta' put should be a winner 30% of the time, or if we sold a 30 delta put, we would expect that we could have a winner 70% of the time. Now, if we can identify a trade that is priced with a 70% win-rate (for example), but find that it wins more often than that, with positive returns, then we have edge — a win that keeps winning.